
O pagină cu toate informațiile despre teoria grafurilor și quiz-uri ajutătoare
Vizitează și celelalte pagini:
Graphviser app
O aplicație pentru vizualizare a algoritmilor din teoria grafurilor.
Pornește aplicația
La ce se folosesc grafurile?
Cu ajutorul grafurilor se pot modela cu succes numeroase aplicații ale matematicii. Poate părea surprinzător faptul că, pe lângă matematică, grafurile sunt utilizate și în industrie, economie, transporturi, în diverse servicii.
Una dintre cele mai cunoscute probleme este cel al comis-voiajorului, care dorește să ajungă în diferite locații prin cel mai scurt (cel mai rentabil) drum posibil. Grafurile sunt perfect potrivite pentru vizualizarea și modelarea diferitelor rute.
Alte aplicații ale grafurilor:
- rețele de apă
- rețele de căi ferate
- rețele de drumuri
- arbori genealogici
- colorarea hărților
Conceptele de bază ale teoriei grafurilor pot fi ilustrate foarte bine printr-un exemplu legat de comunitatea Facebook.
Utilizatorii Facebook sunt vârfurile grafului. Atunci când o persoană lansează o cerere de prietenie, către o altă persoană, intenția de a devenii prieteni, în acel moment nu este reciprocă ci doar unidirecțională, iar această situație se poate ilustra printr-un arc iar graful utilizat pentru reprezentare este un graf orientat.
Dacă cererea de prietenie este acceptată, putem considera, că există arc în ambele direcții între cele două persoane, deci se poate ilustra printr-o muchie. Astfel de relații se pot reprezenta prin grafuri neorientate.
sursă: https://hirmagazin.sulinet.hu/hu/tudomany/grafok-mindenhol
Terminologie
Un graf este o pereche ordonată de mulțimi, notată G =(N, M), unde N este o mulțime finită și nevidă de elemente numite noduri sau vârfuri, iar M este o mulțime de perechi (ordonate sau neordonate) de elemente din N numite muchii (dacă sunt perechi neordonate) sau arce (dacă sunt perechi ordonate). În primul caz, graful se numește neorientat, iar în al doilea se numește orientat.- Adiacență: două vârfuri se numesc adiacente, dacă sunt legate printr-o muchie/printr-un arc.
- Incidenţă: o muchie este incidentă cu un nod dacă îl are pe acesta ca extremitate.
- Incidenţă spre interior: un arc este incident spre interior cu un nod, dacă îl are pe acesta ca vârf terminal (arcul converge spre nod).
- Incidenţă spre exterior: un arc este incident spre exterior cu un nod dacă îl are pe acesta ca vârf inițial (arcul pleacă din nod).
- Buclă: un arc pentru care vârful inițial este identic cu cel terminal.
- Grad: gradul unui nod, dintr-un graf neorientat, este numărul de noduri adiacente cu acesta.
- Grad interior: gradul interior al unui nod în cazul unui graf orientat, este egal cu numărul de arce incidente spre interior.
- Grad exterior: gradul exterior al unui nod, în cazul unui graf orientat, este egal cu numărul de arce incidente spre exterior.
- Nod izolat: un nod cu gradul 0.
- Lanţ: este o secvenţă de noduri ale unui graf neorientat cu proprietatea că oricare două noduri consecutive sunt adiacente.
- Lungimea unui lanţ: numărul de muchii din care este format.
- Lanţ simplu: lanţul care conţine numai muchii distincte.
- Lanţ elementar: lanţul care conţine numai noduri distincte.
- Ciclu: un lanţ în care primul nod coincide cu ultimul.
- Ciclu elementar: ciclul format doar din noduri distincte, excepţie făcând primul şi ultimul.
- Drum: este o secvenţă de vârfuri ale unui graf orientat, cu proprietatea că oricare două vârfuri consecutive sunt adiacente.
- Lungimea unui drum: numărul de arce din care este format.
- Drum simplu: drumul care conţine numai arce distincte.
- Drum elementar: drumul care conţine numai vârfuri distincte.
- Circuit: un drum în care primul vârf coincide cu ultimul.
- Circuit elementar: circuitul format doar din vârfuri distincte, excepţie făcând primul şi ultimul.
- Graf parţial: un graf G1=(N, M1) reprezintă graf parţial al grafului G=(N, M) dacă M1 este inclus în M. Cu alte cuvinte G1 este graf parţial al lui G, dacă este identic, sau se obţine prin suprimarea unor muchii (respectiv arce) din G.
- Subgraf: un subgraf al lui G=(N, M) este un graf G1=(N1, M1) în care M1 este inclus în M, iar M1 conţine toate muchiile/arcele din M care au ambele extremităţi în N1. Cu alte cuvinte G1 este subgraf al lui G, dacă este identic, sau se obţine prin suprimarea unor noduri împreună cu muchiile/arcele incidente cu acestea.
- Graf complet: graf neorientat G=(N, M) în care există muchie între oricare două noduri. Numărul de muchii ale unui graf complet este |N |*|N-1|/2.
- Graf conex: un graf neorientat în care, pentru orice pereche de noduri există un lanţ care le uneşte.
- Graf tare conex: un graf orientat în care, pentru orice pereche de vârfuri (v1, v2) ,există drum de la v1 la v2 şi un drum de la v2 la v1.
- Componentă conexă: subgraf al grafului de referinţă, maximal în raport cu proprietatea de conexitate (între oricare două vârfuri există lanţ).
- Lanţ hamiltonian: un lanţ elementar care conţine toate nodurile unui graf.
- Ciclu hamiltonian: un ciclu elementar care conţine toate nodurile grafului.
- Graf hamiltonian: un graf, care conţine un ciclu hamiltonian.
- Lanţ eulerian: un lanţ simplu care conţine toate muchiile unui graf.
- Ciclu eulerian: un ciclu simplu care conţine toate muchiile grafului.
- Graf eulerian: un graf care conţine un ciclu eulerian.
- Graf ponderat: un graf în care fiecărei muchii/arc îi este asociată o valoare.
Reprezentarea grafurilor
Matricea de incidență
Pentru un graf cu n noduri și m muchii, matricea de incidență este o matrice de ordin n x m și elemente din {0, 1}, cu semnificația:
 , unde
, unde 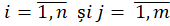
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | |
|---|---|---|---|---|---|---|---|---|
| 1 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 1 |
| 2 | 1 | 1 | 0 | 1 | 0 | 0 | 1 | 0 |
| 3 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 0 |
| 4 | 0 | 0 | 1 | 1 | 1 | 1 | 0 | 0 |
| 5 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 1 |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| 2 | 0 | 0 | 1 | 1 | 0 | 1 | 1 | 0 | 0 | 0 | 0 |
| 3 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 1 | 1 | 0 | 0 |
| 4 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 0 |
| 5 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 1 | 1 |
| 6 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
Observații
Într-un graf neorientat:
- suma elementelor de pe linia i este gradul nodului i;
- suma elementelor de pe orice coloană este 2.
Într-un graf orientat:
- de multe ori est util să se cunoască orientarea arcului, astfel se poate nota cu 1 nodul de ieșire respectiv cu -1 nodul de intrare.
Lista de muchii
Pentru un graf cu n noduri și m muchii, lista de muchii este o matrice de ordin m x 2 și elemente din mulțimea nodurilor. Fiecare linie din matrice conține extremitățile unei muchii.
| 1 | 1 | 2 |
|---|---|---|
| 2 | 2 | 3 |
| 3 | 3 | 4 |
| 4 | 2 | 4 |
| 5 | 4 | 5 |
| 6 | 1 | 4 |
| 7 | 2 | 5 |
| 8 | 1 | 5 |
| 1 | 1 | 6 |
|---|---|---|
| 2 | 3 | 6 |
| 3 | 6 | 2 |
| 4 | 2 | 3 |
| 5 | 1 | 5 |
| 6 | 2 | 5 |
| 7 | 4 | 2 |
| 8 | 3 | 4 |
| 9 | 4 | 3 |
| 10 | 5 | 4 |
| 11 | 5 | 5 |
Matricea de adiacență
Pentru un graf cu n noduri și m muchii, matricea de adiacență este o matrice pătratică de ordin n și elemente din {0, 1}, cu semnificația:
 ,
, 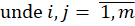
| 1 | 2 | 3 | 4 | 5 | |
|---|---|---|---|---|---|
| 1 | 0 | 1 | 0 | 1 | 1 |
| 2 | 1 | 0 | 1 | 1 | 1 |
| 3 | 0 | 1 | 0 | 1 | 0 |
| 4 | 1 | 1 | 1 | 0 | 1 |
| 5 | 1 | 1 | 0 | 1 | 0 |
Observații
Într-un graf neorientat:
- matricea de adiacență este simetrică față de diagonala principală;
- elementele de pe diagonala principală au valoarea 0;
- suma elementelor de pe linia/coloana i este gradul nodului i;
- suma tuturor elementelor din matrice este egală cu dublul numărului de muchii din graf.
Într-un graf orientat:
- suma elementelor de pe linia/coloana i este gradul exterior/interior al nodului i;
- suma tuturor elementelor din matrice este egală cu numărului de muchii din graf;
- în cazul grafurilor ponderate în locul valorii 1 se trece ponderea (costul) arcului iar matricea se numește matricea costurilor. Valorile 0, care nu sunt pe diagonala principală se înlocuiesc cu o valoare foarte mare.
Lista de adiacențe
Pentru un graf cu n noduri și m muchii, lista de adiacențe este o matrice de ordin n x m și pentru fiecare nod i, i fiind numărul de ordine a liniei din matrice, linia i conține vârfurile adiacente cu nodul i (lista vecinilor lui i).
| 1 | 2 | 4 | 5 | |
|---|---|---|---|---|
| 2 | 1 | 3 | 4 | 5 |
| 3 | 2 | 4 | ||
| 4 | 1 | 2 | 3 | 5 |
| 5 | 1 | 2 | 4 |
| 1 | 5 | 6 |
|---|---|---|
| 2 | 3 | 5 |
| 3 | 4 | 6 |
| 4 | 2 | 3 |
| 5 | 4 | 5 |
| 6 | 2 |
În anumite cazuri este bine să memorăm pentru fiecare nod numărul de noduri adiacente cu el. În acest scop putem folosi coloana 0 din matrice pentru a reține aceste valori pentru fiecare nod (linie) în parte.
| 0 | 1 | 2 | 3 | |
|---|---|---|---|---|
| 1 | 2 | 4 | 6 | |
| 2 | 2 | 3 | 5 | |
| 3 | 3 | 2 | 4 | 7 |
| 4 | 3 | 1 | 3 | 5 |
Transformări între diferite reprezentări
Matricea de adiacență → Matricea de incidență
Matricea de adiacență → Lista de muchii
Matricea de adiacență → Liste de adiacență
Lista de muchii → Liste de adiacență
Matricea de incidență → Lista de muchii
Liste de adiacență → Matricea de adiacență
Matricea de incidență → Liste de adiacență
Liste de adiacență → Lista de muchii
Liste de adiacență → Matricea de incidență
Parcurgerea grafurilor
Parcurgerea în lățime
drum: 1 4 6 3 5 7 2
- Selectăm nodul de pornire și îl plasăm în vectorul coadă drum (și marcăm în vectorul freq).
- Pentru fiecare element plasat în vectorul drum, căutăm vecini săi nevizitați încă (care nu au fost incluși în vectorul drum) și le introducem în coadă.
Structuri de date folosite
- pentru stocarea grafului de exemplu, lista de adiacențe
- variabila drum un vector de tip coadă
- vectorul de frecvență freq care indică dacă un nod a fost vizitat sau nu
- e - indică poziția elementului prelucrat în vectorul drum
- u - indică poziția ultimului element din vectorul drum
| 0 | 1 | 2 | 3 | |
|---|---|---|---|---|
| 1 | 2 | 4 | 6 | |
| 2 | 2 | 3 | 5 | |
| 3 | 3 | 2 | 4 | 7 |
| 4 | 3 | 1 | 3 | 5 |
Parcurgerea în adâncime
drum: 1 4 3 2 7 6 5
- Selectăm nodul de pornire și îl plasăm în vectorul drum și în vârful stivei st (marcăm și în vectorul freq).
- Pentru fiecare element aflat în vârful stivei st, căutăm primul său vecin nevizitat încă (și care nu au fost inclus în vectorul drum) și îl introducem în stivă (și în vectorul drum).
Structuri de date folosite
- pentru stocarea grafului de exemplu, lista de adiacențe
- variabila drum un vector
- variabila st un vector de tip coadă
- vectorul de frecvență freq care indică dacă un nod a fost vizitat sau nu
- e – indică poziția elementului prelucrat din stivă
| 0 | 1 | 2 | 3 | |
|---|---|---|---|---|
| 1 | 2 | 4 | 6 | |
| 2 | 1 | 3 | ||
| 3 | 3 | 2 | 4 | 7 |
| 4 | 2 | 1 | 3 | |
| 5 | 1 | 6 | ||
| 6 | 2 | 1 | 5 | |
| 7 | 1 | 3 |
Drumuri în grafuri
Algoritmul lui Dijkstra
Pentru un graf orientat și ponderat cu n noduri și m muchii, să se determine costurile minime ale drumurilor care au acel nod ca extremitate inițială.
- Selectăm nodul de pornire.
- Vectorul ldrum se inițializează cu lungimile muchiilor incidente cu nodul de pornire, 0 pentru nodul de pornire și o valoare foarte mare pentru nodurile care nu sunt adiacente cu nodul de pornire.
- Căutăm acea valoare minimă din vectorul ldrum pentru care prin nodul corespunzător încă nu am încercat să determinăm drum. Dacă prin acest nod se poate obține un drum mai scurt (cu un cost mai mic), actualizăm elementul corespunzător din vectorul ldrum.
Structuri de date folosite
- matricea costurilor, utilizat pentru memorarea grafului
- vectorul ldrum va conține lungimile drumurilor de la nodul de pornire la celelalte noduri
- vectorul freq care indică dacă un nod s-a folosit pentru determinarea drumurilor minime
ldrum: 8 0 ∞ ∞ 1 ∞
freq: 0 0 0 0 0 0
ldrum: 6 0 3 3 1 9
freq: 1 1 1 1 1 1
Matricea drumurilor
Pentru un graf cu n noduri și m muchii, matricea drumurilor este o matrice pătratică de ordin n și elemente din {0, 1}, cu semnificația:
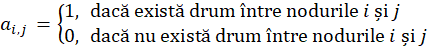 ,
, 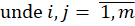
- Pentru a determinarea matricei drumurilor, utilizăm algoritmul Roy-Warshall: dacă nu există drum de la nodul i la j, dar există drum de la i la k și drum de la k la j, atunci se construiește drumul de la i la j, prin reuniunea celor două drumuri existente.
- Graful este memorat cu ajutorul matricei de adiacență.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | |
|---|---|---|---|---|---|---|---|
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 2 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 3 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 4 | 0 | 0 | 0 | 1 | 0 | 1 | 1 |
| 5 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 6 | 0 | 0 | 0 | 1 | 0 | 1 | 1 |
| 7 | 0 | 0 | 0 | 1 | 0 | 1 | 1 |
Algoritmul lui Roy-Floyd pornește de la matricea costurilor și printr-o deducție asemănătoare algoritmului lui Roy-Warshall, determină costul minim al drumurilor între oricare două noduri din graf.
Arborele parţial de cost minim
Pentru un graf neorientat, conex și ponderat cu n noduri și m muchii, se numește arbore parțial un graf parțial al grafului, care este arbore. Se numește arbore parțial de cost minim un arbore parțial pentru care suma costurilor muchiilor este minimă.
Pentru determinarea arborelui parțial de cost minim al unui graf neorientat, conex și ponderat se poate utiliza algoritmul lui Kruskal sau algoritmul lui Prim.
Algoritmul lui Kruskal
- Se ordonează muchiile grafului crescător după cost.
- Considerăm, că inițial fiecare nod face parte dintr-o componentă conexă de sine stătătoare.
- Se analizează pe rând muchiile grafului, în ordinea crescătoare a costurilor. Dacă extremitățile muchiei leagă două noduri, care fac parte din componente conexe diferite, muchia respectivă face parte din arbore iar cele două componente conexe se unifică.
Structuri de date folosite
- pentru stocarea grafului de exemplu, lista de muchii
- vectorul comp cu n elemente și cu semnificația ca nodul i aparține componentei comp[i]
| 1 | 2 | 3 | |
|---|---|---|---|
| 1 | 1 | 4 | 2 |
| 2 | 3 | 5 | 2 |
| 3 | 4 | 6 | 2 |
| 4 | 5 | 6 | 2 |
| 5 | 2 | 5 | 3 |
| 6 | 3 | 4 | 3 |
| 7 | 3 | 6 | 3 |
| 8 | 1 | 6 | 4 |
| 9 | 2 | 3 | 4 |
| 10 | 1 | 2 | 5 |
Algoritmul lui Prim
arborele parţial de cost minim: 3 5 6 4 1 2
- Se stabilește nodul de plecare și se adaugă la arbore.
- Se determină muchia cu ponderea minimă pentru care o extremitate este printre nodurile care au fost adăugate la arbore iar cealaltă extremitate nu aparține arborelui.
- Muchia determinată și extremitatea care nu aparținea arborelui se adaugă la arbore.
- Algoritmul se termină atunci când toate nodurile au fost adăugate la arbore.
Structuri de date folosite
- pentru stocarea grafului de exemplu, lista de muchii
- vectorul freq cu n elemente, freq[i]=1 înseamnă că nodul i aparține arborelui respectiv în caz contrar freq[i]=0
Arbori
- Arbori liberi
Un graf neorientat, conex și aciclic se numește arbore (arbore liber).
Un graf neorientat și aciclic se numește pădure.
- Arbori cu rădăcină
Dacă într-un arbore există un nod special numit rădăcină, iar celelalte noduri sunt ”agățate” de acest nod, graful se numește arbore cu rădăcină.
Caracteristici:
- nivelul: este lungimea unui lanț de la rădăcina la un nod al arborelui (rădăcina se află la nivelul 0);
- înălțime: este lungimea maximă a unui lanț de la rădăcină la un nod al arborelui → în exemplu este 4;
- ascendent, descendent, frați: relația dintre două noduri în funcție de nivelul la care se află două noduri care se află la același nivel sunt frați, un nod aflat pe un nivel cu număr de ordine mai mic este ascendentul nodurilor la care este lanț din acel nod și se află pe nivele cu număr de ordine mai mare iar nodurile respective sunt descendenții nodului; dacă lungimea lanțului este 1, nodul respectiv este descendent direct → în exemplu ascendentul nodului 3 este nodul 1 iar nodul 1 este descendentul lui 3;
- frunză: nodul care nu are niciun descendent → în exemplu nodurile: 4 5 8 9 11 12 13;
- rădăcină: nodul care nu are niciun ascendent → în exemplu nodul 1;
- subarbore: un nod al arborelui împreună cu toți descendenții săi formează un subarbore.
- Arbori binari
Un arbore în care fiecare nod are cel mult doi descendenți se numește arbore binar.
Descendenții se numesc descendentul stânga respectiv descendentul dreapta.
Reprezentarea arborilor cu rădăcină
- Vector de tați
- Scrierea parantezată
Ascendentul direct al fiecărui nod este dat cu ajutorul unui tablou unidimensional. Indicele din vector reprezintă nodul, iar conținutul elementului indică nodul ascendent.
exemplu: figura a.
Pornind de la rădăcină, descendenții fiecărui nod se scriu între paranteze. În cazul nodurilor frunză, între paranteze se scrie caracterul *.
exemplu: figura a. 1 ( 2( 5(*) ), 3( 6(8(*) ), 7(9(*), 10(13(*)), 11(*), 12(*))), 4(*) )
Reprezentarea arborilor binari
- Vector de tați
- Scrierea parantezată
- Reprezentarea standard
- Forma binară
Ascendentul direct al fiecărui nod este dat cu ajutorul unui tablou unidimensional.
exemplu: figura b.
Pornind de la rădăcină, descendenții fiecărui nod se scriu între paranteze. Dacă un nod are un singur descendent, în locul descendentului lipsă se scrie caracterul *.
exemplu: figura b. 1 ( 2(4(8,*), 5), 3(6(9,10(11,12)), 7(*,13)) )
Se specifică nodul rădăcină, apoi pentru fiecare nod se memorează descendentul stânga și descendentul dreapta cu ajutorul a doi vectori sau folosind o matrice de 2 linii și n coloane (n fiind numărul de noduri). Nodul este indicat prin indicele din vector (indicele coloanei din matrice). Dacă nodul nu are descendenți se trece valoarea 0.
exemplu: figura b.
Nodurile arborelui binar le specifică printr-un șir de cifre 0 și 1. Rădăcina se notează cu 1. Pentru un nod prezența cifrei 0 în șir semnifică apartenența la subarborele stâng respectiv cifra 1, apartenența la subarborele din dreapta.
exemplu: (1,1) (2,10) (3,11) (4,100) (5,101) (6,110) (7,111) (8,1000) (9,1100) (10,1101) (11,11010) (12,11011) (13,1111)
Parcurgerea arborilor binari
- Traversarea în preordine (RSD): se vizitează rădăcina, se traversează subarborele stâng, se traversează subarborele drept
- Traversarea în inordine (SRD): se traversează subarborele stâng, se vizitează rădăcina, se traversează subarborele drept
- Traversarea în postordine (SDR): se traversează subarborele stâng, se traversează subarborele drept, se vizitează rădăcina
exemplu: D A C K G P L B F O M I H
exemplu: C A G K P L D F O B I M H
exemplu: C G L P K A O F I H M B D
Arborele binar de căutare
Fiecare nod din oricare subarbore din stânga este mai mic decât rădăcina subarborelui respectiv.
Fiecare nod din oricare subarbore din dreapta este mai mare decât rădăcina subarborelui respectiv.

